ブーメランはどのように投げたら戻って来るのだろうか？横投げ（サイドスロー）ではダメで上投げ（オーバースロー）しなければならないことは、デモンストレータの常識だが、それだけで戻ってくるのだろうか？

1枚の羽の長さがｌ、全体の重さがｍの4枚ばねのブーメランを考えよう。重力による効果は無視することとする。このブーメランを重心速度ｖ、角速度ωで投げたとする。（ここで、ｖ＝ωｌの関係が必ずしも成り立っていないことに注意する。）

ブーメランの慣性モーメントＩと角運動量Ｌは

 

 







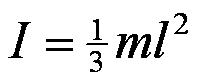
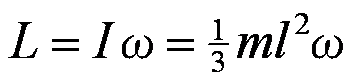
である。ブーメランは横倒しになったコマのようなもので、Ｌは進行方向に向かって左に倒れている。

さて、羽根で生じる揚力はｖ^2に比例する。また、回転しているのだから(ωl)^2に比例する項も付け加えられる。単位長さあたりの揚力係数（の半分）をｃと置けば、4枚の羽根の合力は、

 

 

 

 

 

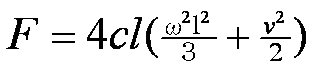
である。また、羽根の上になっている部分と下になっている部分では対地速度が異なるので、揚力の大きさが異なり、そのため力のモーメントが生じるその大きさは、

 

 

 

 

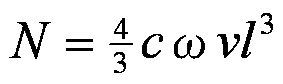
である。

Ｎの向きは常にＬに垂直であり、最初は進行方向と反対向きである。この力のモーメントＮのためＬの方向が刻一刻と変っていき、ブーメランは歳差運動を起こす。Ｌの向きは水平面内を上から見て時計と反対周りに回転することになる。

その回転角速度をωpとすると、ωp=N/Lだから、

 

 

 

となる。
　さらに、ブーメランがが角速度ω0で半径Ｒの円軌道を描いて旋回するとすればｖ＝Ｒω0で、ωpはω0に等しくなければならない。故に

 

 

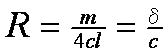
となる。ただし、δ＝ｍ/(4ｌ)は羽根の線密度である。この式からブーメランの旋回半径は投げる速度には依らないことが分かる。ブーメランの旋回半径を決めるのは投げ方ではなく、羽根の線密度と揚力係数だけであり、それらはブーメランの形状や質量と関係している。

　さらに、旋回の向心力はＦであり、投げた場所に戻ってくるのならＦ＝ｍｖ^2/Ｒが成り立っているはずだから、ここから重心速度ｖとブーメランの回転速度（角速度）ωの関係が出てきて、

 

 

 

 

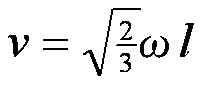
となる。
　つまり、投げた位置に戻ってくるためにはωｌの約0.8倍の（重心の）速さでブーメランは投げられなければならない。このとき上端は進行方向に2.3ｖ、下端は-0.3ｖの速さになっている。このように投げるためには手首のスナップを利かせて投げなければならない。

 

「あら、奥さん」投げというのは静岡科学館る・く・るの海野弘光氏の付けた名前である。
　海野氏が子供達にブーメランの投げ方を指導していたときに、「スナップをきかせて」「手首を使って、こう・・・」と説明しても、余り理解されず、なかなかうまく投らげれないことが多かったそうである。外でボール投げ、特に野球のような遊びをほとんどしなくなった子供達にはスナップをきかせて投げるというのが難しいのであった。
　そこで、この動きに似ている日常行動は何かないかと考えたときに、ドラマやバラエティーなどでおばさんが使う「あら、奥さん！」という動作がほとんど同じであることに気づいて、こう教えたのだそうである。
　あまり小さいと、この「あら、奥さん」を見たこともない子供もいるので、そういうときは、「ブーメランでこんにちはとさせてごらん」という「こんにちは投げ」を使っているそうである。