Python で月食計算

Python で月食計算 (PyEphem版)

PyEphem を用いると、月食が起こる時刻を計算することができます。
（なお、月食が起こる概略の日時は既知のものとします。）

参考にしたページ：
Eclipse Calculations using Python
GitHub - Various scripts to calculate eclipses

必要モジュールをインポートします。

import ephem
import datetime
import numpy as np
from operator import itemgetter

計算を開始する日時を設定します。日時は、世界時で指定します。

initial_date = datetime.datetime(2021, 5, 26, 9, 0, 0, 0, tzinfo=datetime.timezone.utc)

観測者のインスタンス（ここでは observer）を作成します。
観測者の高度を -6371000m として、地球の中心に設定します。大気差は0にします。
作成した観測者 observer に、計算を始める日時を設定します。

observer = ephem.Observer()
observer.elevation = -6371000
observer.pressure = 0
observer.date = initial_date

太陽と月のインスタンス（ここではsun, moon）を作成します。

sun = ephem.Sun()
moon = ephem.Moon()

結果を入れる配列を初期化します。

results = []

これより初期時刻から1秒ずつ時間を進めながら、太陽と月の位置、および地球の本影の計算を繰り返します。
月食の継続時間は最大でも4時間程度のため、ここでは15000秒分、計算します。
太陽と月の大きさ（sun.size, moon.size）の単位は、角度の秒です（直径およそ1800秒=0.5度）。

for x in range(0, 15000):
    osaka.date = initial_date + datetime.timedelta(seconds = x)
    sun.compute(osaka)
    moon.compute(osaka)
    r_sun = sun.size/2
    r_moon = moon.size/2

次に太陽と月の視差を計算します。
視差は (地球半径)/(太陽または月までの距離) で計算できます。
角度を秒の単位にするために3600を掛けています。

    parallax_sun = np.rad2deg(ephem.earth_radius / (sun.earth_distance * ephem.meters_per_au)) * 60 * 60
    parallax_moon = np.rad2deg(ephem.earth_radius / (moon.earth_distance * ephem.meters_per_au)) * 60 * 60

視差から、地球の本影の視半径を求めます。
本影の視半径は (太陽の視差)+(月の視差)-(太陽の視半径) で計算できます。（下図）
地球の本影の視半径の大きさは、大気による屈折で約1/50大きくなることから、51/50 を掛けています。

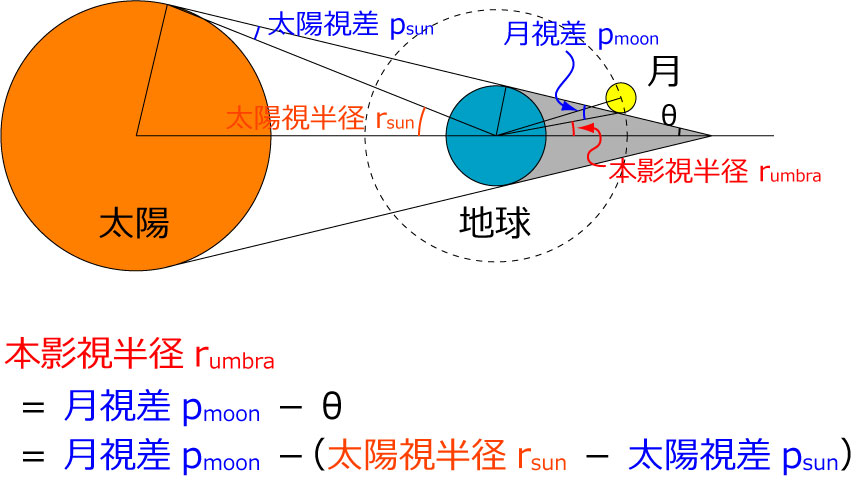
    umbra = (parallax_sun + parallax_moon -r_sun) * 51/50

次に月と地球の本影の角距離を計算します。
本影は太陽の反対側になるので、太陽と月の角距離を求めて180度を引きます。
角距離は separation メソッドを使うことで、簡単に計算できます。
separation メソッドで計算される角度の単位は度なので、秒の単位にするために3600を掛けています。

    s = abs(np.rad2deg(ephem.separation(sun, moon)) - 180) * 60 * 60

食分を計算します。食分がプラス（(umbra + r_moon) > s ・・・地球の本影と月の半径の和よりも、本影中心と月の角距離が小さい）なら、月が欠けています。

    percent_eclipse = (umbra + r_moon - s) / (r_moon * 2)

計算結果（時刻、食分）を配列 results に追加します。

    results.append([ephem.localtime(observer.date), percent_eclipse])

食分の最大値と、その時刻を探します。
配列 results の1番目の要素の最大値が、食分の最大値です。

max_eclipse = max(results, key = itemgetter(1))

print('食の最大:', max_eclipse[0])
print('最大食分: {0:.2f}'.format(max_eclipse[1]))

欠け始めと食の終わりの時刻を探します。
最初に食分が0以上になった時刻が欠け始め（第一接触）、再び食分が0になった時刻が食の終わり（第四接触）です。

eclipse = False

for x in results:
    if x[1] > 0 :
        if eclipse == False:
            print('欠け始め:', x[0])
            eclipse = True
    else :
        if eclipse == True:
            print('食の終わり:', x[0])
            eclipse = False

計算結果

食の最大: 2021-05-26 20:18:42
最大食分: 1.02
欠け始め: 2021-05-26 18:44:26
食の終わり: 2021-05-26 21:52:57

全体は次のようになります。

import ephem
import datetime
import numpy as np
from operator import itemgetter

# 初期時刻設定
initial_date = datetime.datetime(2021, 5, 26, 9, 0, 0, 0, tzinfo=datetime.timezone.utc)

# 観測地設定
observer = ephem.Observer()
observer.elevation = -6371000
observer.pressure = 0
observer.date = initial_date

# 太陽・月
sun = ephem.Sun()
moon = ephem.Moon()

# 結果のリストを初期化
results = []

# 1秒ずつ4時間分　計算繰り返し
for x in range(0, 15000):
    # 時刻を1秒進める
    observer.date = initial_date + datetime.timedelta(seconds = x)

    # 太陽・月の位置・半径計算
    sun.compute(observer)
    moon.compute(observer)
    r_sun = sun.size/2
    r_moon = moon.size/2
    
    # 視差・本影の視半径計算
    parallax_sun = np.rad2deg(ephem.earth_radius / (sun.earth_distance * ephem.meters_per_au)) * 60 * 60
    parallax_moon = np.rad2deg(ephem.earth_radius / (moon.earth_distance * ephem.meters_per_au)) * 60 * 60
    umbra = (parallax_moon -r_sun + parallax_sun) * 51/50

    # 月・地球の本影の角距離の計算
    s = abs(np.rad2deg(ephem.separation(sun, moon)) - 180) * 60 * 60

    # 食分の計算
    percent_eclipse = (umbra + r_moon - s) / (r_moon * 2)

    # 計算結果を追加（時刻、食分）
    results.append([ephem.localtime(observer.date), percent_eclipse])

# 食の最大の検索	
max_eclipse = max(results, key = itemgetter(1))
    
print('食の最大:', max_eclipse[0])
print('最大食分: {0:.2f}'.format(max_eclipse[1]))

# 欠け始めと食の終わりの検索
eclipse = False

for x in results:
    if x[1] > 0 :
        if eclipse == False:
            print('欠け始め:', x[0])
            eclipse = True
    else :
        if eclipse == True:
            print('食の終わり:', x[0])
            eclipse = False

江越 航のホームページ

Python で月食計算 (PyEphem版)

　江越　航のホームページ